Exploring Advanced Machine Learning with Multilayer Perceptrons

The single-layer perceptron is conceptually simple and the training process is relatively easy. However, it is not capable of handling complex real-world applications. A common way to explain its basic limitations is to use Boolean operations as an example, which I will employ in the text.

Neural network logic gates

It is interesting to note that we use an extremely complex microprocessor to implement a neural network that functions in the same way as a circuit consisting of a few transistors. However, considering the problem from this point of view emphasizes the inadequacy of single-layer perceptrons in general-purpose classification and function approximation. If our perceptron cannot replicate the behavior of a single logic gate, it is time to look for a better perceptron.

system configuration.

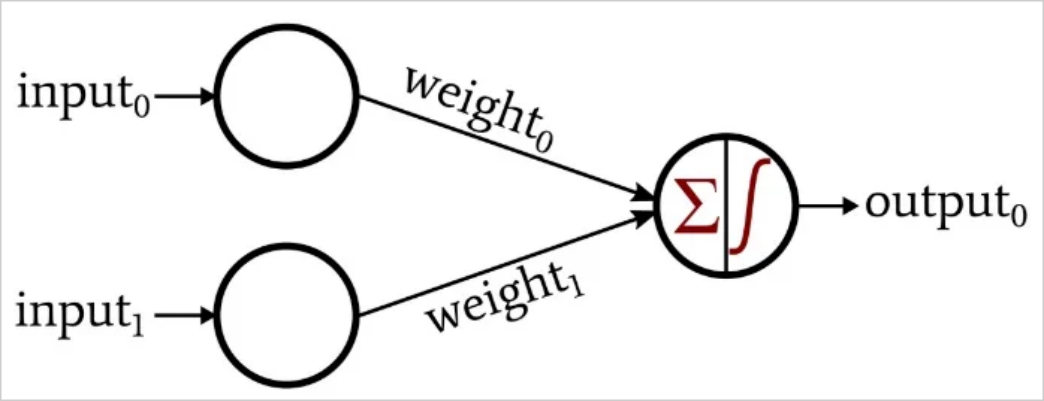
The shape of this perceptron reminds me of a logic gate, and indeed, soon it will be such a gate. Suppose we train this network with samples of input vectors containing zeros and ones, and the output value is one only when both inputs are one. In this way, this neural network can simulate the behavior of an AND gate.

The input dimension of this network is 2, so we can simply plot the input samples on a two-dimensional graph. Suppose input0 corresponds to the horizontal axis and input1 to the vertical axis. The four possible input combinations are arranged as follows:

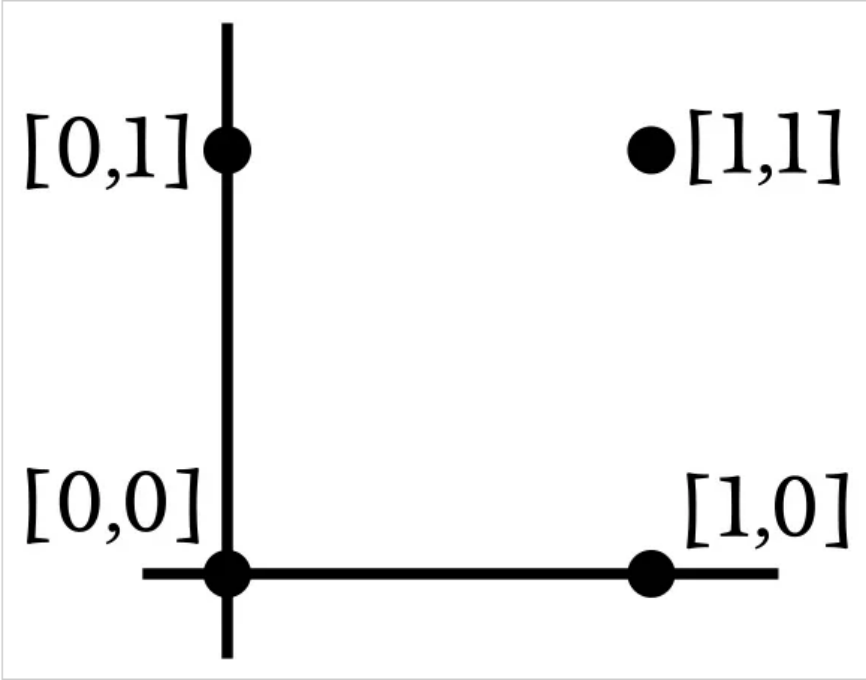
Since we are replicating the AND operation, the network needs to adjust its weights so that the output is 1 for the input vector [1,1] and 0 for the remaining three input vectors.Based on this information, we partition the input space into regions corresponding to the desired output classification:

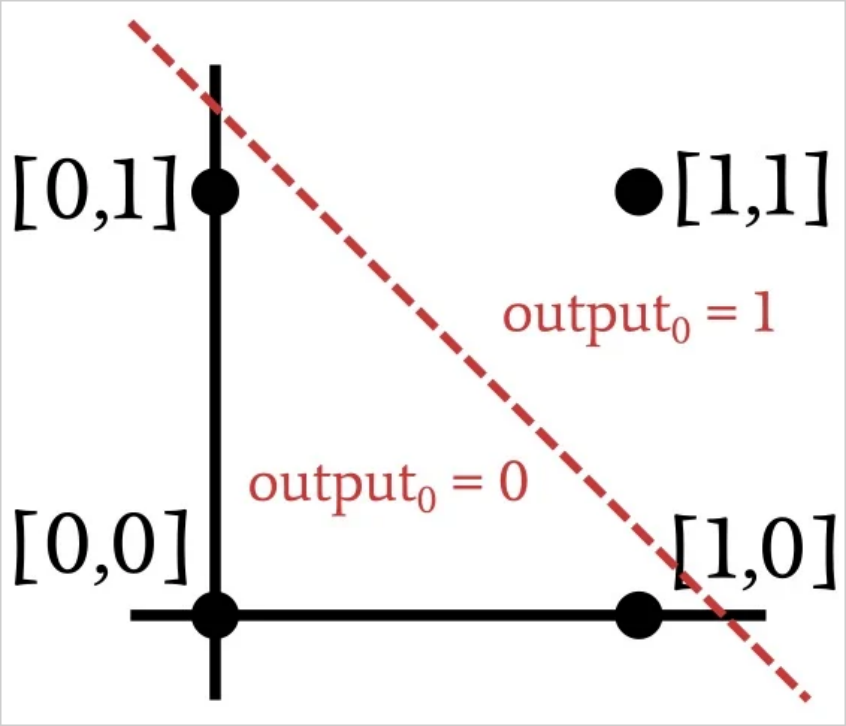
Linearly Classifiable Data

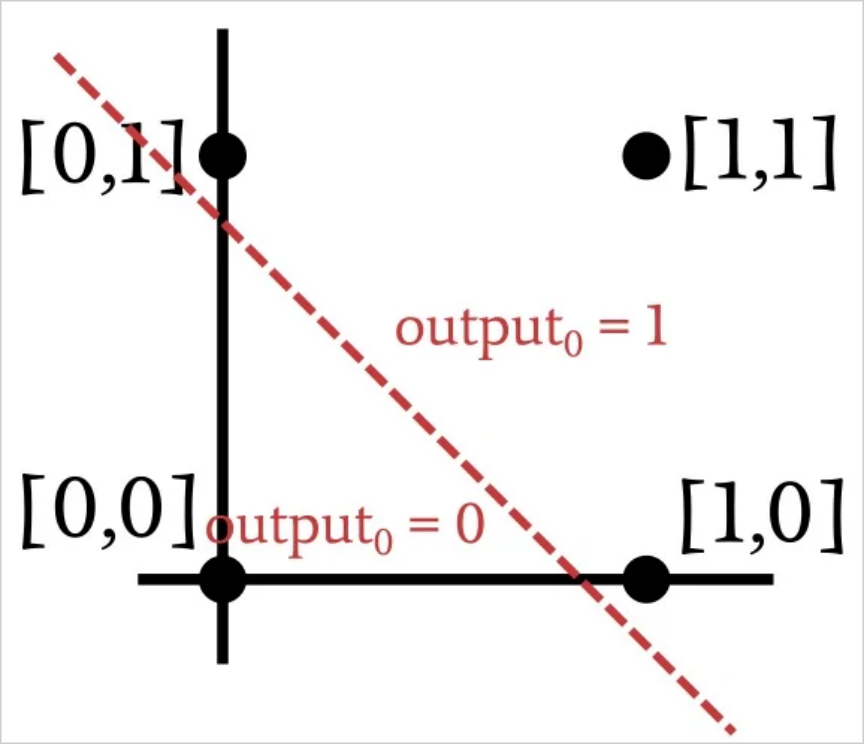
As shown in the previous figure, when we implement the AND operation, we can classify the plotted input vectors by drawing a straight line. One side of the line has an output of 1 and the other side has an output of 0. Thus, in the case of the AND operation, the data provided to the network is linearly differentiable. The same is true for the OR operation:

It turns out that a single-layer perceptron can only solve the problem where the data is linearly divisible. This case is independent of the dimension of the input samples. The two-dimensional case is easy to visualize because we can plot points and separate them with lines. In order to generalize the concept of linear separability, we must use the term “hyperplane” instead of “line”. Hyperplanes are geometric features that can separate data in n-dimensional space. In a two-dimensional environment, a hyperplane is a one-dimensional feature (i.e., a line). In a three-dimensional environment, a hyperplane is a regular two-dimensional plane. In an n-dimensional environment, a hyperplane has (n-1) dimensions.

Solving the problem of nonlinear differentiability

During training, the single-layer perceptron tries to find out the location of the classification hyperplane based on the training samples. When it finds hyperplanes that can reliably segregate the data into the correct classification, it can be put into practical use. However, when such a hyperplane does not exist, the perceptron will not be able to find it. Let's look at an example where the input to output relationship is not linearly separable:

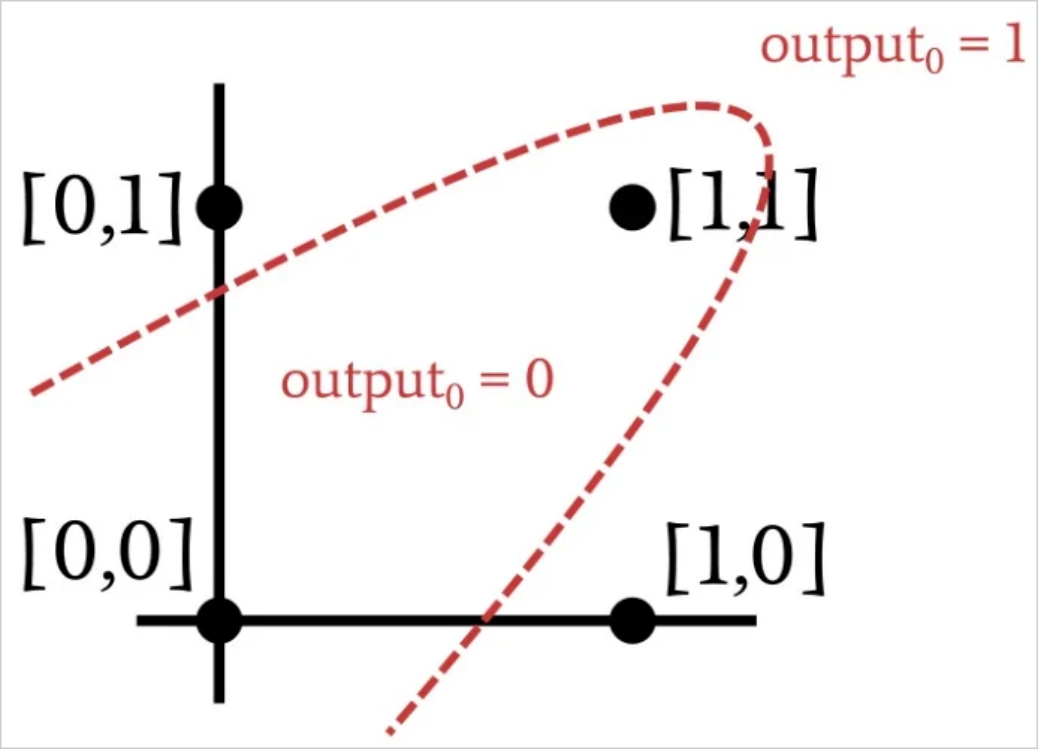
Do you recognize the relationship? Look a little closer and you'll see that this is an XOR operation. You can't separate XOR data with a straight line. As a result, the single-layer perceptron is unable to realize the functionality provided by the XOR gate, and if it can't perform the XOR operation, it's reasonable to assume that many other (and more interesting) applications will outgrow the problem-solving capabilities of the single-layer perceptron.

Fortunately, by adding just one node layer, we can greatly enhance the problem-solving capabilities of the neural network. This will turn the single-layer perceptron into a multilayer perceptron (MLP). As mentioned in previous posts, this layer is called a “hidden layer” because it has no direct interface with the outside world. I guess you can think of the MLP as a “black box” that accepts input data, performs mysterious mathematical operations, and outputs the data. The hidden layer is inside this black box. You can't see it, but it's there.

Conclusion

Adding a hidden layer to a perceptron is a relatively simple way to improve the overall system, but we can't expect to get this enhancement at no cost. One of the first drawbacks that comes to mind is that the training process becomes more complicated